Word-break Memoization Solution

Conquer Dynamic Programming in 3 easy steps – Part 2

by Gil Vegliach

This is the second blog post that explains how to tackle dynamic programming. Part 1 explains how to derive a recursive solution. Now it’s time to optimize it.

We will use memoization (top-down dynamic programming) to improve the time complexity of the solution. We will continue from part 1 using the problem word-break as example.

Dynamic programming is a useful topic for coding interviews. For a complete preparation course, I recommend Tech Interview Pro by ex-Google, ex-Facebook Senior Staff Software Engineer Patrick Shyu (the Tech Lead). Use this links to get 40% off and support the blog. And for more popular coding interview problems, check out CoderPro. Use this link to get 20% off.

Step 2: Memoization (caching)

Memoization is a simple caching technique. By storing the results of expensive function calls, you avoid recomputing them, lowering the time complexity. Obviously, it works only if there are overlapping subproblems.

The steps to apply memoization are:

  1. Create a new hashtable. Keys correspond to function’s parameters, values correspond to the function’s return type.
  2. Create a new helper function that takes all parameters of the original function plus the hashtable. Move the recursive code here.
  3. In the original function call the new helper function with the hashtable.
  4. Adjust the recursive part:
    • In the first line check the cache.
    • Before every “return”, write the result to the cache.

Let’s see this process in action with the word break problem.

In part 1, we were left with this (skeleton of the) code:

def wordBreak(s, dict):
  if s in dict:
    return True
  for ...:
    ...
    if ...:
      return True
  return False

Applying the steps above:

  1. Create a new hashtable string -> boolean.
  2. Create a new function wordBreakCached(string, dictionary, cache) and move the code here.
  3. Call wordBreakCached() from wordBreak().
  4. Check the cache when entering wordBreakCached() and update the cache when exiting wordBreakCached().

This leads to the following (skeleton of the) code:

def wordBreak(s, dict):
  return wordBreakCached(s, dict, {})

# Additional function with cache
def wordBreakCached(s, dict, cache):
  if s in cache:
    return cache[s];
  if s in dict:
    cache[s] = True
    return True
  for ...:
    ...
    if prefix in dict and wordBreakCached(suffix, dict, cache):
      cache[s] = True
      return True
  cache[s] = False
  return False

Although the exponential complexity is optimized away, this solution still times out on LeetCode. On LeetCode wordDict is a list (corresponding to dict here) and checking containment in a list is O(n). The easy fix is wrapping the list in a (hashed) set.

Step 2a: Optimizations and prep for Part 3

Although the tests pass now, we can further optimize the code removing useless string hashing. Since the cache keys are strings, on every cache access all the bytes of the strings are processed.

This is not necessary because we process only substrings of a fixed string s. In fact we can represent substrings with pairs of indices (l, r). Using pairs as cache keys leads to faster hashing: O(1) vs O(len(s)).

This optimization is not only cosmetic: it’s also a preparation step for part 3 that employs bottom-up dynamic programming.

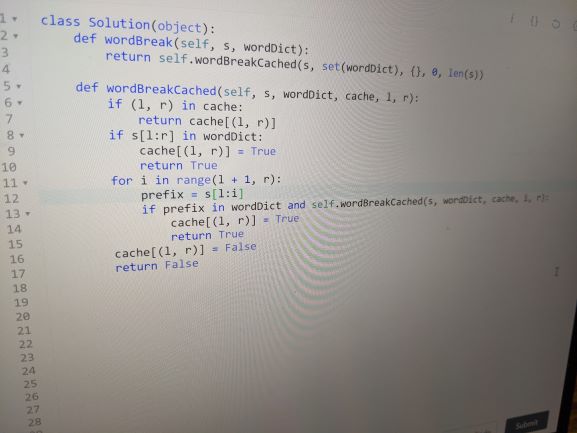
def wordBreak(s, dict):
  return wordBreakCachedFast(s, set(dict), {}, 0, len(s))
        
def wordBreakCached(s, dict, cache, l, r):
  if (l, r) in cache:
    return cache[(l, r)]
  if s[l:r] in dict:
    cache[(l, r)] = True
    return True

  for i in range(l + 1, r):
    if s[l:i] in dict and wordBreakCached(s, dict, cache, i, r):
      cache[(l, r)] = True
      return True
    cache[(l, r)] = False
    return False

Many already call this code dynamic programming. Theoretically speaking, we reached the best time complexity. Practically speaking, though, the code performs many recursive calls which bring overhead (e.g. pushing and popping parameters on the callstack). So it’s often convenient to rewrite the algorithm in a bottom-up fashion.

This will be done in Part 3 and it’s what many consider the final form of dynamic programming.

Dynamic programming is a useful topic for coding interviews. For a complete preparation course, I recommend Tech Interview Pro by ex-Google, ex-Facebook Senior Staff Software Engineer Patrick Shyu (the Tech Lead). Use this links to get 40% off and support the blog. And for more popular coding interview problems, check out CoderPro. Use this link to get 20% off.

Other resources