Conquer Dynamic Programming in 3 easy steps – Part 3

This is the third blog post explaining how to tackle dynamic programming. Part 1 deals with the recursive solution. Part 2 uses memoization to decrease the time complexity. This final part will use tabulation to make the code cleaner and even faster.

Bottom-up dynamic programming, also known as tabulation, is the fastest-in-practice way to code up your dynamic programming algorithms. The speed gains derive from avoiding both recursion and hashing by changing the order of iteration and using a simple (multi-dimensional) array instead of a hash table.

In this blog post, we will optimize further our solution to word-break from Part 2, turning the code from top-down dynamic programming (memoization) to bottom-up dynamic programming (tabulation).

Dynamic programming is a useful topic for coding interviews. For a complete preparation course, I recommend Tech Interview Pro by ex-Google, ex-Facebook Senior Staff Software Engineer Patrick Shyu (the Tech Lead). Use this links to get 40% off and support the blog. And for more popular coding interview problems, check out CoderPro. Use this link to get 20% off.

Step 3a: Code clean-up and prep

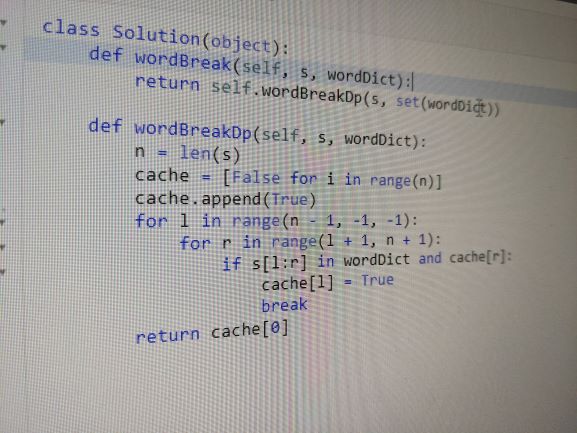
In part 2, we were left with this code:

def wordBreak(s, dict):
  return wordBreakCachedFast(s, set(dict), {}, 0, len(s))

def wordBreakCached(s, dict, cache, l, r):
  if (l, r) in cache:
    return cache[(l, r)]
  if s[l:r] in dict:
    cache[(l, r)] = True
    return True
  for i in range(l + 1, r):
    if s[l:i] in dict and wordBreakCached(s, dict, cache, i, r):
      cache[(l, r)] = True
      return True
    cache[(l, r)] = False
  return False

Before applying bottom-up dynamic programming, it’s useful to simplify further. The first thing to notice is that the parameter r has a constant value in all call sites. This means it is useless and can be removed:

def wordBreakCachedFast(s, wordDict, cache, l):
  if l in cache:
    return cache[l]
  if s[l:] in wordDict:
    cache[l] = True
    return True
  for i in range(l + 1, len(s)):
    prefix = s[l:i]
    if prefix in wordDict and wordBreakCachedFast(s, wordDict, cache, i):
      cache[l] = True
      return True
    cache[l] = False
  return False

Cache[i] now tells whether the suffix s[i:], and not arbitrary substrings, can be split using words from wordDict. This simplification is important because it will make the cache a simple list instead of a 2d matrix in the bottom-up version.

Step 3: Bottom-up dynamic programming

To go from top-down to bottom-up, let’s pause for a moment and think about the order of recursive calls. They form a tree traversed in post-order. The following diagram shows the call stack for wordBreak(“abcd”, { “a”, “b”, “bc”, “d”}).

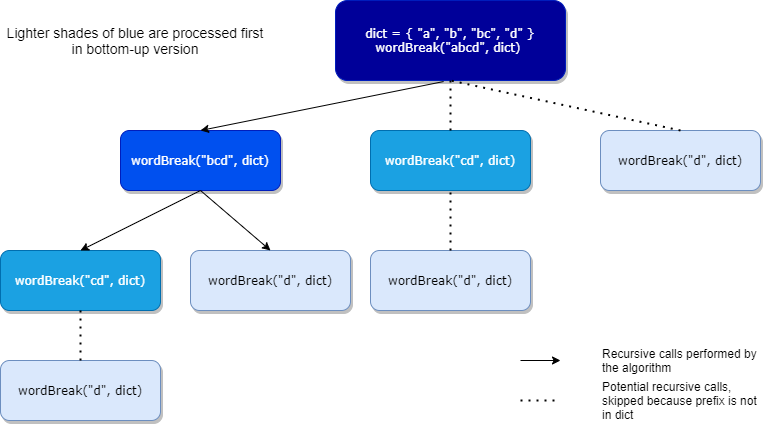
NB: “Potential branches” are drawn with dotted lines. The algo skips these branches because prefix is not in dict. For illustration purposes, let’s pretend these calls are carried out as if the algorithm used the non-short-circuited &.

The key idea for bottom-up dynamic programming is to unravel the recursion tree and go bottom-up, i.e. go layer by layer from the leaves to the root. In the diagram, we go from the lightest to the darkest shade of blue: First process wordBreak(“d”, dict), then wordBreak(“cd”, dict), then wordBreak(“bcd”, dict) and finally wordBreak(“abcd”, dict). The code becomes:

def wordBreakDp(s, dict):
  n = len(s)
  cache = [False for i in range(n)]
  cache.append(True)
  for l in range(n - 1, -1, -1):
    for r in range(l + 1, n + 1):
      if s[l:r] in dict and cache[r]:
        cache[l] = True
        break
  return cache[0]

The distinct points to notice here are:

cache is not a dictionary but a simple list of booleans (easier to cache in CPU cache lines).
The recursive call has been replaced by a cache check (cache and dictionary checks can be swapped to avoid creating useless substrings).
There is an additional for-loop on index r that checks whether a suffix can be split.
The result is stored in cache[0], i.e. the base case.
An additional True was added to cache to simplify the code when a suffix is present in the dictionary without trailing characters.

This post concludes the mini-series on dynamic programming. Leave a comment to let me know your thoughts, e.g. clarifications and/or more problems.

Step 3a: Code clean-up and prep

Step 3: Bottom-up dynamic programming

Other resources