In today’s blog post I will break down dynamic programming, a fundamental CS topic that throws off many programmers at first.
Dynamic programming is feared as an advanced topic in software engineering interviews and CS classes. But it is quite simple if you know the steps to crack it. In this blog post, I will use the classic word-break problem to show the method to tackle such problems.
Leave a comment if you are interested in other problems.
A dynamic programming problem and can be approached in 3 steps:
- Derive a recursive solution (this post).
- Cache with memoization.
- Bottom-up dynamic programming.
This post (step 1) deals with the hardest step, i.e. coming up with a recursive solution. It also explains how to recognize a dynamic programming problem (step 0).
Dynamic programming is a useful topic for coding interviews. For a complete preparation course, I recommend Tech Interview Pro by ex-Google, ex-Facebook Senior Staff Software Engineer Patrick Shyu (the Tech Lead). Use this links to get 40% off and support the blog. And for more popular coding interview problems, check out CoderPro. Use this link to get 20% off.
Step 0: Recognize dynamic programming
Dynamic programming is a “caching technique” for recursive algorithms. It can be used only under two conditions:
- Optimal sub-structure: An optimal solution can be build from optimal solutions of sub-problems (i.e. a divide-and-conquer algorithm).
- Overlapping sub-problems: The same sub-problems occur multiple times during the computation of the solution (and therefore can be cached away).
The first condition doesn’t have anything to do with caching and it describes a sub-class of recursive solutions. These algorithms are also called divide-and-conquer. A simple example is merge-sort: You can sort an array by sorting its two halves and merging them together. To apply this condition you need to have a recursive formulation of your solution.
The second condition is where the magic happens and what will get your solution from exponential time complexity to polynomial time (and space) complexity. Caching the overlapping sub-problems is mechanical work and you will be spending most of your time coming up with a recursive algorithm. As an example, merge-sort doesn’t have overlapping sub-problems, because you never sort again the same sub-array, but problems as word-break, coin change or edit distance do.
Step 1: Recursive solution
The secret to figure out the recursive solution is to take for granted you have a function that works on a smaller input and then try to use the same function to solve the original problem.
You approach this as a dialog with yourself or with an interviewer. Then you tweak your recursive solution till it works.
The general steps are:
- Name a function and its parameters.
- What-if assumptions on which parameter gets smaller and how.
- Try out examples and see if it leads to a solution.
- If it doesn’t work, why? Repeat from step 2.
- Formulate a precise solution (e.g. with math) and argument why it works (e.g. with a proof). If it doesn’t work, repeat from step 1.
Example: Word-break problem
Word-break on leetcode: “Given a non-empty string s and a dictionary dict containing a list of non-empty words, determine if s can be segmented into a space-separated sequence of one or more dictionary words.”
Let’s see how the algorithm above works for word-break. You tell yourself:
“I need a function wordBreak(s, dict). Now I assume this function works on a smaller input. What does smaller input mean? In this case, either a shorter string or a smaller dictionary.”
Both are valid guesses and, in many cases, you will try both. For brevity’s sake, let’s do it on a shorter string which leads to the solution. So you go on and repeat it to yourself once more, with more details:
“I have a function wordBreak(t, dict) that tells me whether t can be segmented with words in dict, where t is substring in s (actually subsequence). How can I use this function to segment s?”.
Well you try the obvious first, so you tell yourself: (first Eureka moment)
“Well if t were very long, almost as long as s, I’d be almost done. What if t were basically s without the first letter?”
At this point, you go on and try some examples. For instance if s=”aprettycat” and dict={“a”, “pretty”, “cat”, … } you can break off “a” checking the dictionary; then t=”prettycat” and you know your solution will work (by assumption).
But you try different examples and this doesn’t always work. This works only when the prefix of s is in the dictionary (second Eureka moment):
“Well, I can test if a “prefix of s” is in dict, then set suffix=”rest of s” and know that wordBreak(suffix, dict) tells me true/false if suffix can be segmented. If I test all possible prefixes of s, this will cover all possible segmentations”.
In mathematical notation this is:
wordBreak(s, dict) := true iff
there exists a prefix of s, i.e. s=concat(prefix, suffix),
where prefix is in dict AND wordBreak(suffix, dict) = true.
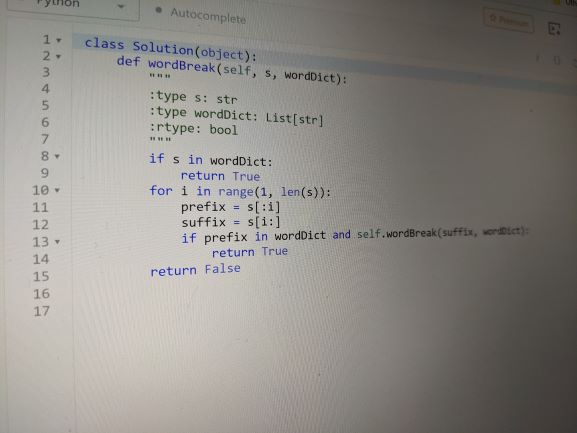
In code you test for all prefixes with a for-loop:
def wordBreak(s, dict):
# Base case of recursion
if s in dict:
return True
# Loop through al prefixes...
for i in range(1, len(s)):
prefix = s[:i]
suffix = s[i:]
# Mathematical formula
if prefix in dict and wordBreak(suffix, dict):
return True
return False
The next blog post, i.e. part 2, will explain memoization and bottom-up dynamic programming. Leave a comment below if you interested in other topics/problems.
Finally, dynamic programming is a useful topic for coding interviews. For a complete preparation course, I recommend Tech Interview Pro by ex-Google, ex-Facebook Senior Staff Software Engineer Patrick Shyu (the Tech Lead). Use this links to get 40% off and support the blog. And for more popular coding interview problems, check out CoderPro. Use this link to get 20% off.